My last blog post was about how to solve Sudoku with Simple Data Science Tricks such as backtracking, it was smart, however, what if in a project like this we don’t have access to the optimal method? Can we use machine learning methods to search for a good solution?

In this blog post, I will show you two independent machine learning methods in solving Sudoku puzzles, one is Genetic Algorithm, the other is Simulated Annealing. Both of them are search algorithms aiming to find the optimal solution by iteratively evaluating the current solution and update the search by comparing against the previous round of solution.

Note that neither of these two approaches is guaranteed to find the best/correct solution, but they can find a close form solution relative quickly.

Metric to measure how good a solution is (loss function)

Before thinking about what approach to use, it is important to come up with a measure for the accuracy of a solution.

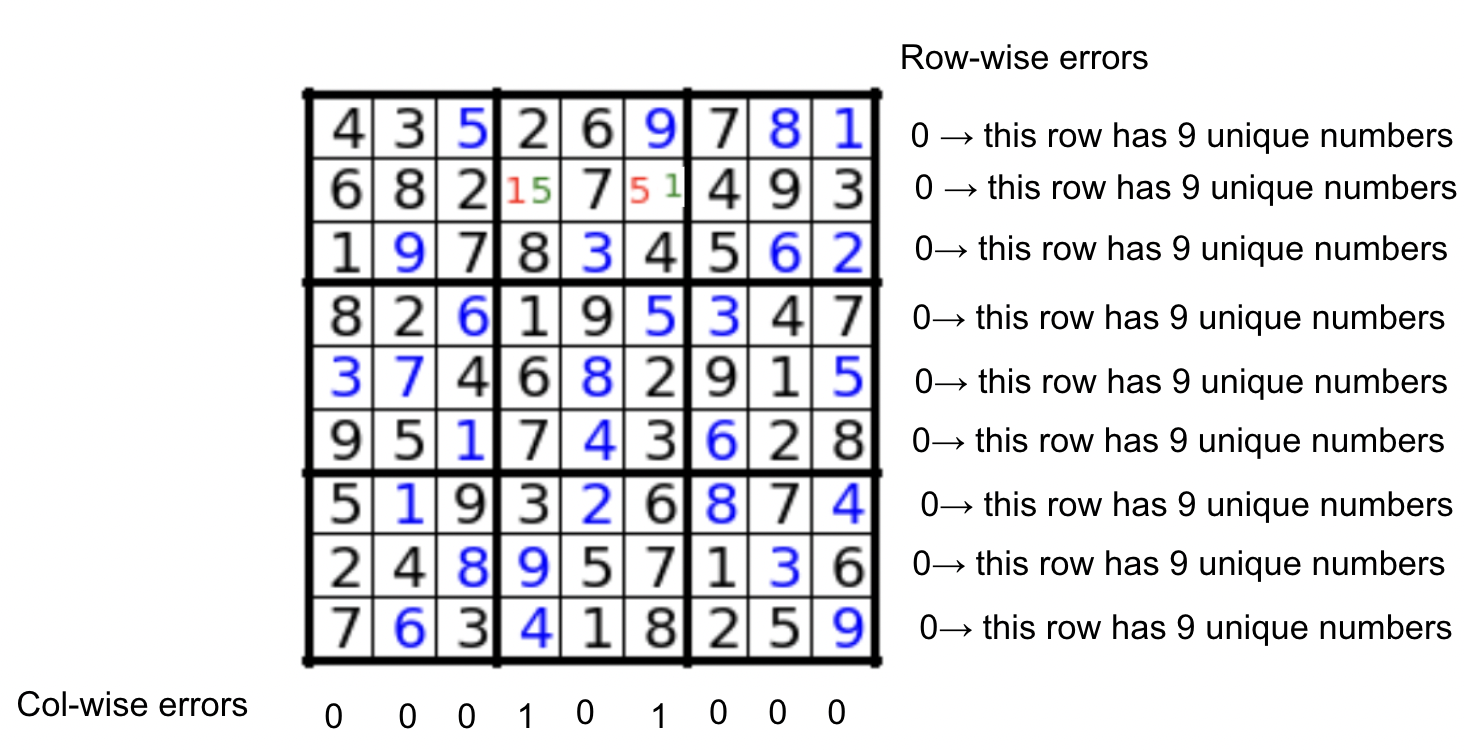
In both methods shown here, Sudoku is solved by filling each block with nine unique numbers, this means only the column and row constraints would need to be checked. Below is the formula I used to measure the overall accuracy of a potential solution, the correct solution should have a value 0, meaning there are no overlapping numbers for each row or column.

The quality of a potential solution = number of overlapping numbers row-wise + number of overlapping numbers column-wise

The below example has a quality score of 2. (black: given puzzle, blue: correctly predicted numbers, red: incorrectly predicted numbers, green: correct number of incorrectly predicted position)

Genetic algorithm

The genetic algorithm mimics the natural evolution, where for each generation (iteration), a fixed number of solutions (e.g N = 100, N is also called a population) are generated and evaluated, the ones with the greatest fitnesses (e.g top 30%, 100 x 30% = 30 solutions, also called elites) are going to be kept to the next generation. The rest of the solutions of the next generation are made with cross-overs and mutations. Cross over is done by taking a percentage of two randomly sampled solutions from the current generation to form a new solution, we can form some (e.g 35) solutions this way. Mutation can be done by randomly swapping two numbers from a chosen block using solutions from the current generation pool, we can form some (e.g 35) solutions this way. The next generation will then have 100 solutions (30 elites from the previous generation, 35 from crossing over, 35 from mutations).

The below figure illustrates my implementation of a cross-over and a mutation. Mutation is done by swapping.

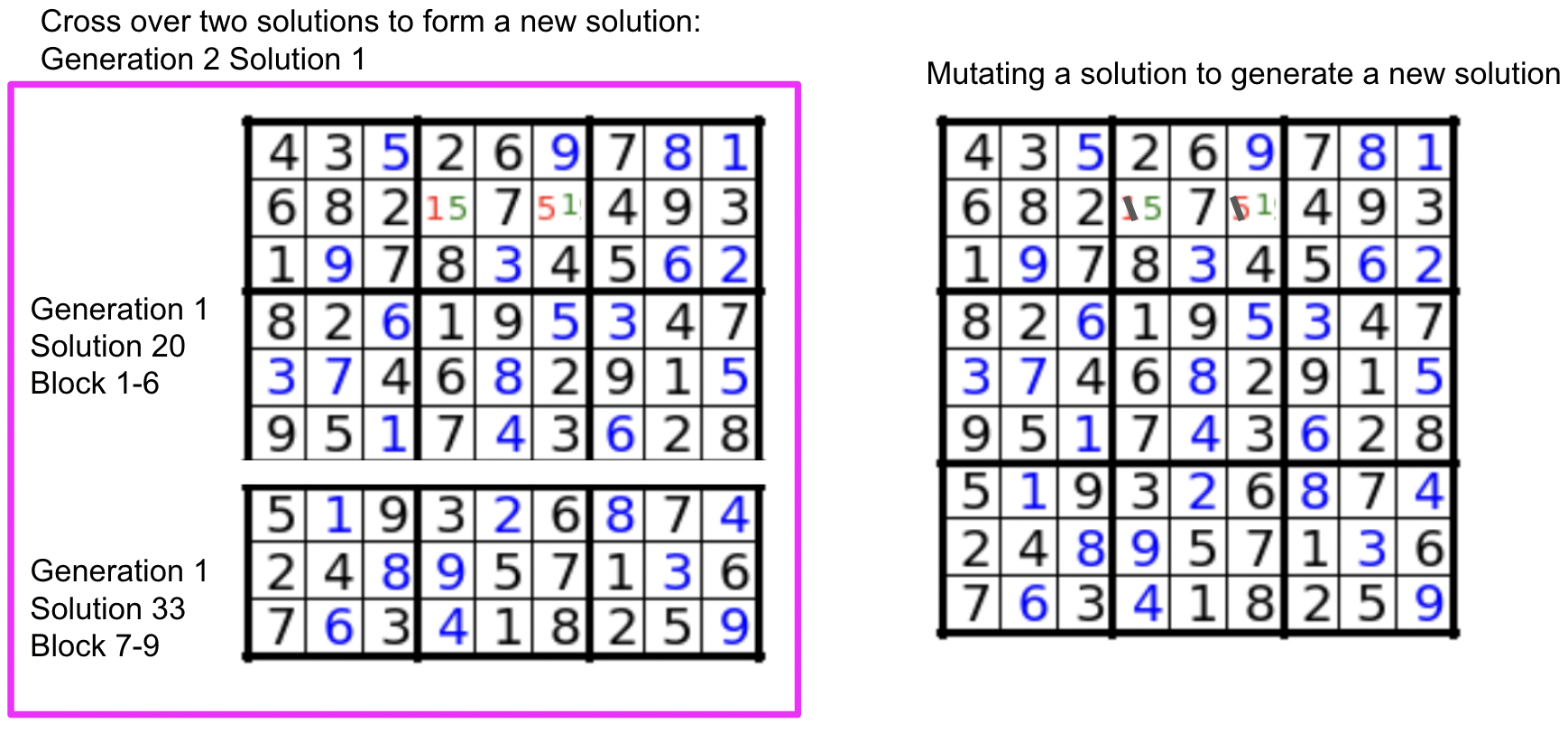
While elite solutions from a generation are kept to the next generation to ensure good minimum performances, crossing over and mutations are done to generate additional and potential better solutions.

Therefore, the best performer of the next generation Soduku solutions would be better or at least the same as the best performer from the current generation. When the top performer from a generation has no rol-wise and col-wise error, we find the answer to the puzzle.

I compared the results of solving three Sudoku puzzles with different difficulties using the genetic algorithm, you can find them in this notebook. In summary, it is able to find a solution quickly in simple puzzles, however, for difficult ones, it is likely trapped in the suboptimal search space.

Simulated annealing

Different from the genetic algorithm, where a population of solutions are generated and optimized in each generation in search of a better solution, simulated annealing is an iterative procedure that continuously updates one candidate solution until a termination condition is reached. You can find the comparison of two algorithms in this paper.

Simulated annealing is a simple algorithm: the candidate solution is updated if the new solution generated is better than the candidate solution (measured by the loss function) or by random chance. In the beginning of the “annealing” process while the “temperature is hot”(temperature is a parameter set by the user), the “shape of the iron” is more flexible (the search space for different solutions is big), therefore, a new solution would have a higher chance to be accepted even if the solution proposed is not better than the candidate solution. This gives more opportunity to the algorithm to explore in the early stage. As the “temperature slowly cools down” after each iteration, the probability of accepting a random solution went down, so the algorithm is forced to find solutions that are better than the candidate solution.

Simulated annealing is a stochastic process and people often adjust the ‘cooling process’ to speed up finding a good solution.

I compared the results of solving three Sudoku puzzles with different difficulties using the simulated annealing algorithm in this notebook. It is less efficient than the genetic algorithm probably because of the limited exploration it has within each iteration.

What could be done to increase the precision of the algorithms?

I realized that the loss function used here might not have represented how close a candidate solution is to the correct one. Given the wrong configurations would sometimes give lower column or row errors than the configurations that are closer to the real answer, maybe it is time to think about using a different loss function. For example, with access to both puzzles and answers, we can certainly measure how far the current candidate to the correct answer is.

In my next blog post, I plan to show you using a graph neural network to predict the correct Sudoku solutions. Stay tuned!

Other resources

The approaches implemented in this blog post is inspired by the following:

A Youtube video on using simulated annealing in solving Sudoku puzzle

A GitHub repo on solving Sudoku with genetic algorithm