In the recent weeks I’ve been learning about JAX, a Python library for machine learning developed by Google Research team and extensively used by Deepmind.

What is JAX and why is it different?

JAX uses Numpy based API for numerical computation. It has three main features making it attractive for fast and simple deep learning model implementation:

• Auto-differentiation (a.k.a grad in JAX) for customized functions. This means when optimizing loss for a machine learning model, instead of having to derive gradient and code it yourself or using syntactic and semantic constraints, the grad function will just compute the gredient for you based on the loss function.

• Fast and efficient vectorization and parallelization (a.k.a vmap and pmap in JAX). Like numpy vectorization, it simplifies the coding process and speeding up computation drastically.

• Just-in-time (JIT) compilation (a.k.a jit in JAX). I think this is the main secret sauce for JAX to perform so much faster than other packages, take a look at the comparisons in quick start on jit and combine jit with vmap.

Resources to learn about JAX

Tutorial: JAX 101 from JAX docsfile is a great point to start, though I found a bit challenging to understand some examples as a beginner.

My mentor plus friend Eric Ma wrote a gradient-based machine learning course called dl-workshop, which uses JAX framework to illustrate machine learning concepts.

Robert Tjarko Lange has several blog posts on using JAX on deep learning based projects, while Colin Raffel demonstrated key concepts of JAX in You don’t know JAX with code.

How does vmap() function work?

According to JAX docsfile on vmap, jax.vmap(function, in_axes=0, out_axes=0) returns a function which maps the function one specified over using in_axes and stack them together using out_axes . The concept is simple but it took me a while to understand when in_axes or out_axes is not set as default.

To understand what it is really doing when in_axes and out_axes change, I’m creating simple arrays with unique numbers in matrix forms called a and b and passing them into a simple function numpy.sum(axis=None) to do default element-wise addition.

• Let’s see an example with in_axes as default.

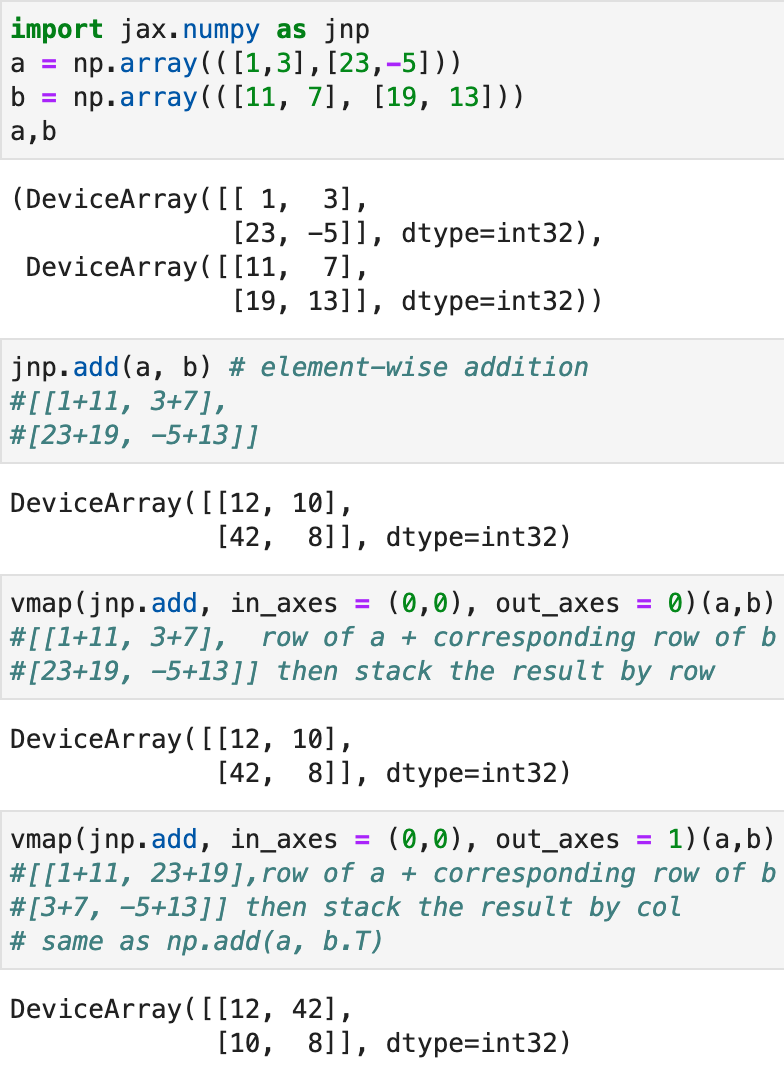
The in_axes is a tuple with two number, since there are two inputs a and b. in_axes[0] indicates which axis to focus on for a, it can take in different values: None, 0 or -2 (map over 0th axis also known as -2 axis in this case, the operation will be performed row-wise), 1 or -1 (map over 1st axis also known as -1 axis in this case, the operation will be performed col-wise). Given a only has two dimensions, there won’t be any additional axis available for vmap to work on. in_axes[1] can take in four different values same as in the case of a, but the computation would be on b. Note at least one input in in_axes should be integer instead of None. out_axes simply means how one would like to stack the results, either by row ( as 0) or column (as 1).

• Change in_axes to customized integers, what would the function return?

The operation is done on the specified axis. Overall, if in_axes has all integers, the shape of the output remains the same as of (2,2) just like what you would see in regular np.add(a,b).

• Mutate some integer in in_axes to None (note that at least one of the input should be integer), what would the result be like?

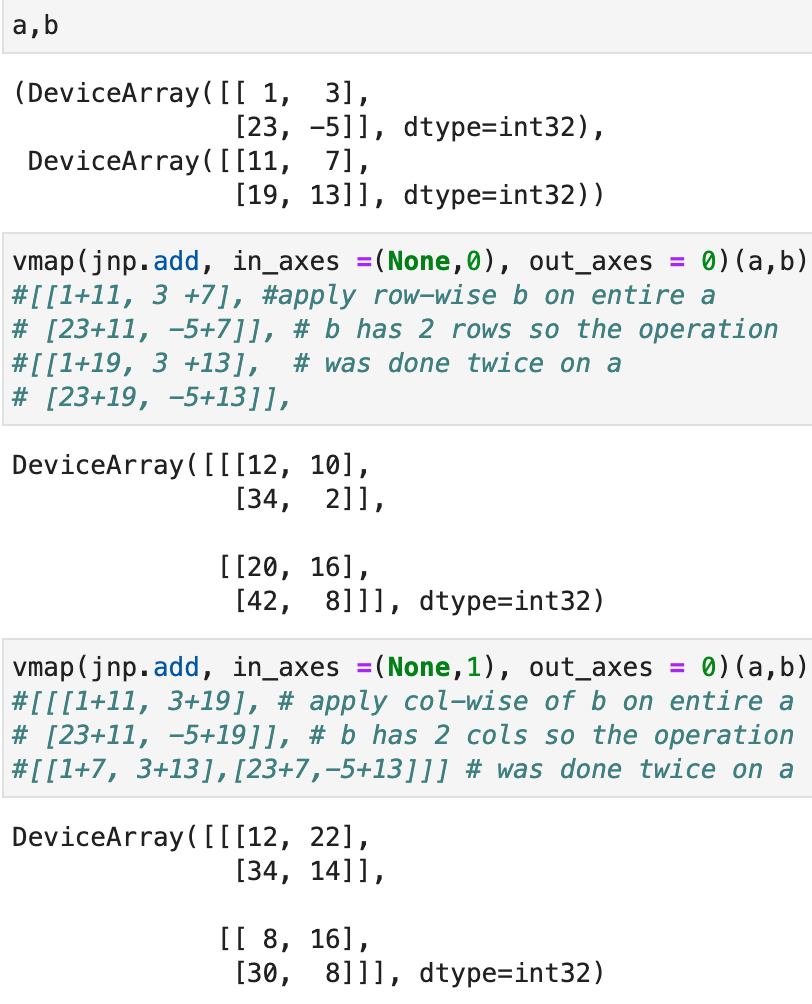
The example outputs are all of shape (2,2,2) instead of the original shape (2,2), why is that? We see the in_axes for a is always None, this indicates the operation is going to pick whatever axis specified in b and apply it on the all rows of a. Given a is of shape (2,2) and b has two rows and two columns, you can think of each operation produced two copies of a, then apply row or col of b on a.

• A more complicated example

The above example is simple, each input is of the same shape and has two dimensions. What if we have two matrices each of shape (2,3,5,7,9)? What would we expect when changing the in_axes? Note that although a and b matrices are initiated differently, they have the same shape.

Based on user supplied function, only inputs with matching dimensions will work together. Try vmap(jnp.add, in_axes = (0, 1) , out_axes = 0 )(a,b).shape it would tell you 0-axis of a is of size 2 while 1-axis of b is of size 3, therefore, the computation can’t happen. Then it is obvious that the operation takes out whatever axis specified and stack them as 0-th axis.

Let’s set one of the in_axes as None and change the out_axes.

You realized there is an additional axis in the output just like in the simple example. But the returned shape can be a bit confusing. Is there a pattern? I summarized the pattern in an intuitive way in the table below, though it might also be possbile to infer the output shape in a different way. First, write down the output shape when out_axes=0. Then, sequentially swap output axes. The output shape of out_axes ==n equals to swapping the (n-1)th index with nth index in out_axes ==(n-1) shape.

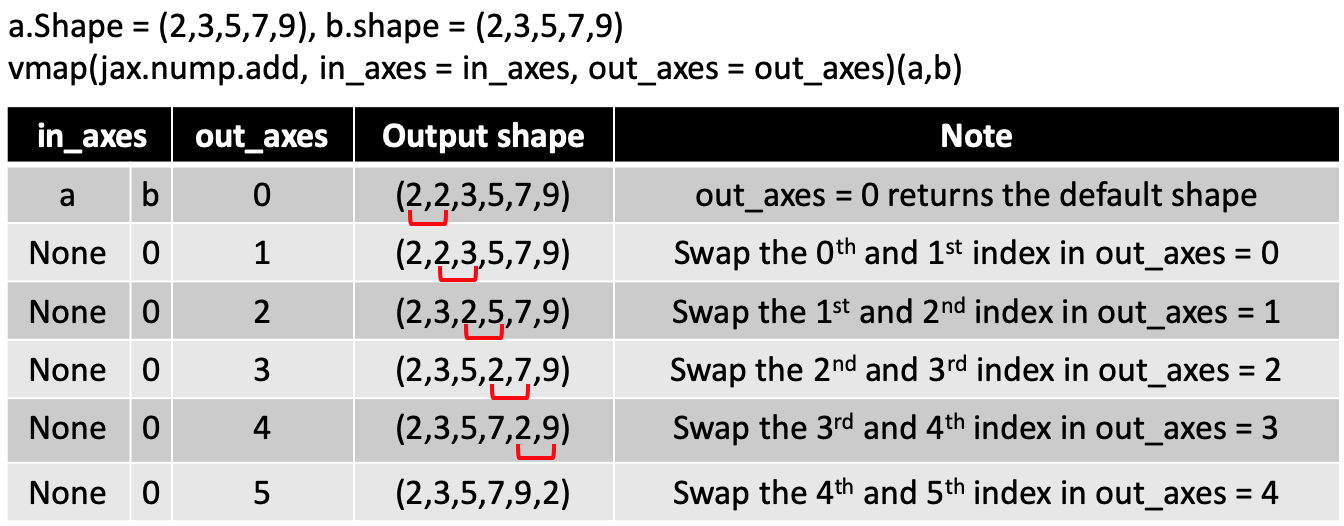
Summary of in_axes and out_axes in vmap()

Imagine you have two matrices that the customized function is applied on, A1 is of shape (a1,b1,c1,….) with x dimensions, A2 is of shape (a2,b2,c2,….) with y dimensions, and the output has z dimensions.

1. The values used for in_axes: in_axes = (x',y'), where x’ is an integer between [-x, x), y is an interger between [-y, y). x’ or y’ can also be None, but at last there should be one integer value in (x’, y’).

2. The scenario of in_axes = (n,None) will apply take out the nth index from the first matrix and apply (1, remianing shape of the first matrix…) on the 2nd matrix. e.g A1.shape = (a1,b1,c1), A2.shape = (a2,b2,c2). in_axes = (1,None) will apply vectors of shape (1,a1,c1) to all rows in A2, while in_axes = (2,None) will apply vectors of shape (1,a1,b1) to the all rows in A2.

3. out_axes is an interger of value between (-z, z].

4. To figure out the change of shape when you change out_axes: First, write down the output shape when out_axes=0. Then, sequentially swap output axes. The shape of the output for out_axes ==n equals to swapping the (n-1)th index with nth index in out_axes ==(n-1) output shape.

I want to thank Arkadij Kummer for giving valuable advice on making this blog post easier to understand :) .